二、一些基本觀測參數的量測原理

隨著積體電路以及計算機科技的快速發展，各種輕、薄、短、小的電子產品紛紛問世；在此趨勢下，當代海洋研究船上幾乎所有的探測儀器均不可避免地全被電子式裝備取代。我們在上一節曾列出了一些常見的，例如溫度、鹽度、壓力、流速等等海洋觀測參數，那麼這些電子式裝備又是經過什麼樣的過程將真實世界裡物理參數的變化轉化成為我們可以眼見的數字記錄呢？這個過程可以藉由下圖(摘自 Wikipedia Data acquisition)來說明；圖中綠方塊代表真實世界裡物理參數(Physical System)的變化，這些物理性的變化經由紫色方塊所示之傳感器(Transducer Sensor)感應後轉化成為類比式的電子訊號，後者再傳給灰色方塊之訊號處理單元(Signal Conditioning，可能包括訊號放大、電位調整、濾波等等不同的電路組合)，經處理過後再傳給粉紅方塊的類比/數位轉換器(Analog-Digital Converter，就是將類比訊號轉成為數位的積體電路)轉化成為數位訊號，最後送交給淺藍色方塊所示之計算機(Computer)做儲存、運算或另作計算處理；此處所謂之Computer只是泛稱，除各型電腦外，亦包括各式各樣的微處理器(Micro-processor)以及DSP (Digital Signal Processor，有時一個DSP便可完全處理後三段流程)等。幾乎所有當代電子式海洋儀器主要的資料擷取(Data Acquisition)架構都可以用這樣的方塊圖來呈現。

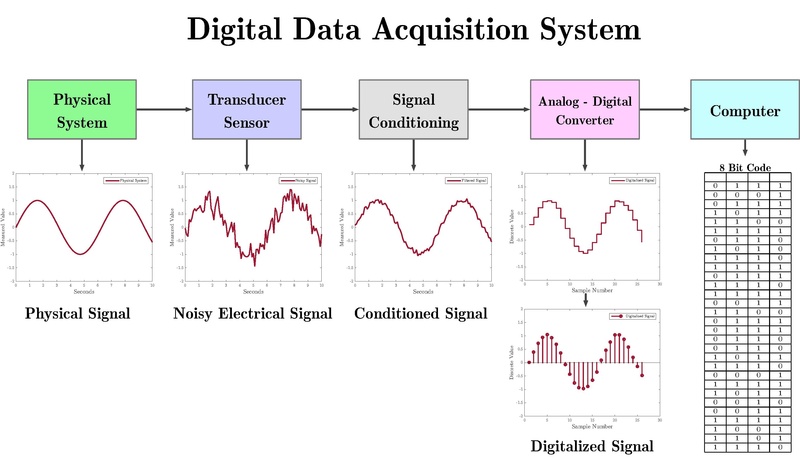
資料擷取系統方塊圖(摘自 Wikipedia Data acquisition)

我們就以國內各研究船必備的溫鹽深儀(Conductivity-Temperature-Depth，CTD)為例來說明傳感器(Transducer)。CTD就是海洋學三個重要觀測參數-導電度、溫度以及深度的縮寫簡稱，以下就按這三個參數反過來的順序來敘述。

(一)壓力感應器(Pressure Sensor)

海洋儀器多用壓力大小來換算為深度，常用之壓力感應器不外下列三種型式，

(1)應變計(Strain Gauge)式：應變計是一種具特殊形狀、可以黏貼在受測物體上的金屬薄片，當物體受到應力產生形變時，(貼在受測物體上的)應變計的電阻就會相應發出微量改變，藉用惠斯通電橋(Wheatstone bridge)可以量測電阻變化而推知應力大小。下圖即為一個典型的薄片型應變計，摘自 Wikipedia Strain Gauge。

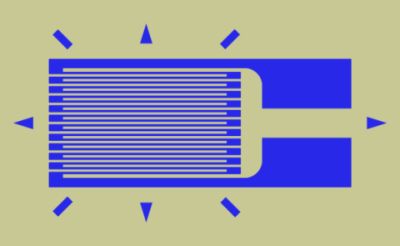一個典型的薄片型應變計，摘自 Wikipedia Strain Gauge。

(2)壓阻IC(Piezoresistive IC)式：材料受到機械式應力時其電阻會發生變化，這種效應稱為壓阻效應(Piezoresistive effect)。半導體材料亦會有壓阻效應，應用半導體壓阻特性作為壓力感應器而產製之IC稱為壓阻IC。下圖為壓阻IC照片(摘自 Wikipedia Pressure sensor)。

壓阻IC照片(摘自 Wikipedia Pressure sensor)。

以及(3)壓電晶體(Digiquartz)式：利用石英晶體受到壓力作用變型因而改變振盪頻率的特性(壓力改變→晶體變形→電容改變→RC振盪頻率改變，式中R為電阻，C為電容)，藉助計數器(counter)量測頻率即可得出壓力數值(digit)(此種壓力感應器為Paroscientific公司設計生產，Digiquartz®為其商標)。

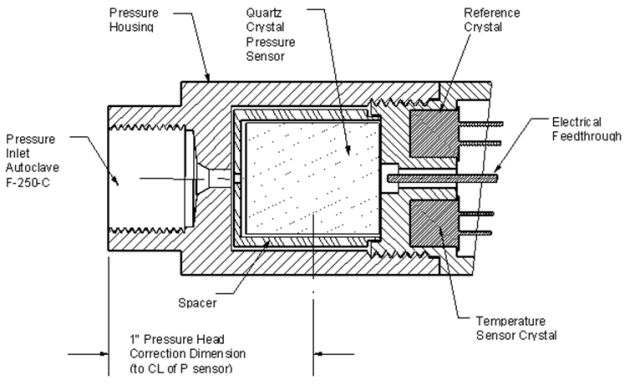Digiquartz壓力感應器內部構造(摘自Quartzdyne公司網頁)

Paroscientific Digiquartz®深水型深度計，最大可量測深度可達7000m，精確度(accuracy)為最大量測範圍之0.01%。摘自Paroscientific, Inc. - Depth Sensors

就準確性(Precision)以及精確度(accuracy)比較：Digiquartz (0.01% FS) > Piezoresistive IC (0.1% FS) > Strain Gauge  (FS: Full Scale)。就價格比較：Digiquartz > Piezoresistive IC > Strain Gauge 。一般深水型(作業深度可達6000m或以上)儀器所使用之壓力感應器多採用壓電晶體型，淺水型儀器(如淺海潮位計、淺海壓力式測波儀等)則多使用壓阻 IC型或應變計型感應器。

(二)溫度傳感器(Temperature Transducer)

常用的溫度傳感器有下列四種，

(1)熱電偶(Thermocouple)：1821年德國物理學家Thomas Johann Seebeck在電磁實驗中發現由兩種不同金屬做成的接點加熱時，會產生電流，這種由熱會產生電的現象稱為熱電性(Thermo-electricity)；隨後(1831年)A.C. Becquerel發現可以利用此種熱電性來量測溫度。現在將席貝克 －柏克勒爾(Seebeck—Becqerel)接點稱為熱電偶。熱電偶是由兩種不同的金屬或不同的材料(如陶瓷及半導體材料)於其中一端熔接在一起而組成。(引自「徐綱鴻 溫度原理」)

熱電偶一例 (K-Type -40~250℃裸接點熱電偶，摘自廣華電子商城網頁)

(2)熱敏電阻(Thermistor)：是一種具有電阻會隨溫度變化而改變的半導體元件；多由蒸發薄膜，碳或碳的混合物，或者是由銅、鈷、錳、鎂、鎳或鈾的氧化物形成之似陶瓷的半導體製作而成。熱敏電阻可以做成各種不同的形狀，應用甚為寬廣，下列二圖顯示兩種不同形狀的熱敏電阻。(引自「徐綱鴻 溫度原理」) 熱敏電阻的溫度係數為負(即電阻會隨溫度增高而降低)。

GE奇異10KΩ立式負溫度係數熱敏電阻(引自廣華電子商城網頁)	1Ω 30A NTC負溫度係數熱敏電阻(引自廣華電子商城網頁)

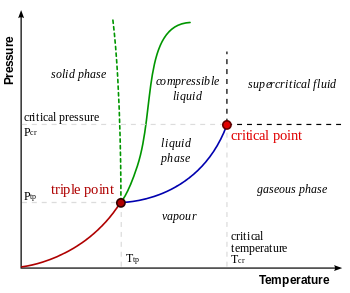
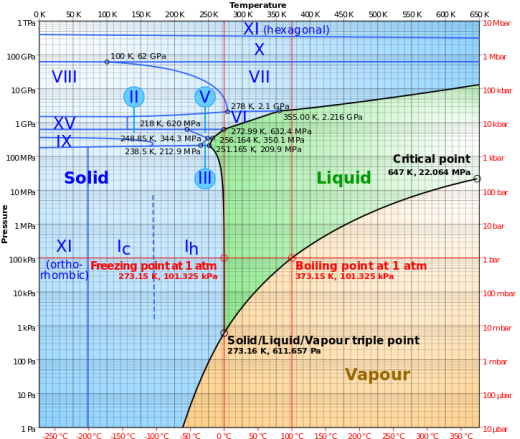
(3)白金電阻式溫度感測器(Resistance Temperature Detector，RTD)：以白金製的 RTD元件，其電阻變化對溫度之比(ΔR/T)為0.377％Ω /℃，而且在0℃及100℃範圍內具有直線性，精確度為±0.001℃。 在測溫中，均採用白金製 RTD元件作為國際標準，國際白金溫度刻度(IPTS)用氧的沸點(-183.962℃)至銻的熔點(+630.74℃)當標準白金RTD元件。另一新標準(IPTS-68)其參考端點為氫的三相點(13.81K)及銻的凍結點。(以上引自「徐綱鴻 溫度原理」) 海洋儀器溫度校正常用的兩個參考點分別為水的三相點 0.01 °C (氣壓為4.56 mm Hg，即0.006 atm)以及鎵(Gallium)的三相點 29.7666 °C。(註：三相點 triple point是指在一個特定的溫度以及特定的壓力下，某物質可以三相(氣態、液態以及固態)同時並存的狀況，下左為某物質之相變(phase diagram)及三相點示意圖，下右則為水的相變圖，參閱 Wikepedia Triple point)。絕大多數具備穩定、線性以及可重複等特性的RTD元件都是由白金製成，白金RTD的溫度係數為正(如下下圖)，其電阻值要比熱敏電阻小很多，例如典型的熱敏電阻在25°C 時約為1 MΩ ，但各種白金RTD在0°C 時電阻值範圍為25Ω 至 1 kΩ 之間，100Ω 的白金RTD在線性度以及可重複性上表現最好(引自Bonnie Baker 2011: Designing with temperature sensors)。

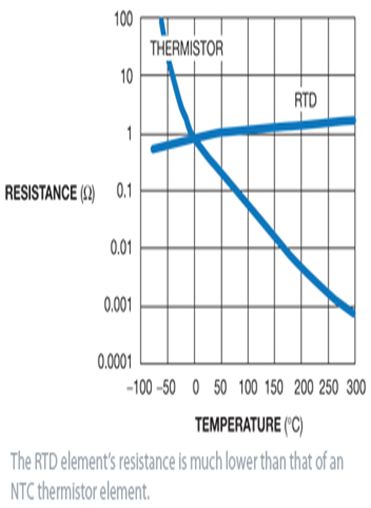RTD元件的電阻值遠小於熱敏電阻(引自Bonnie Baker 2011: Designing with temperature sensors)。

一個典型的白金RTD元件，以下為原廠說明： The TT363 is an integrated platinum RTD temperature sensor with 4-20mA current loop output. Combines transmitter capability with a platinum sensing element in a single package for an easier-to-install temperature sensing solution. Power and signal are provided through a 4-20mA current loop connection. Sensor measuring and operating range is from -50 to 300°F (-45.5 to 148.9°C). The high-temperature plastic case and electronics can be used in applications with an ambient temperature up to 185°F (85°C). Connection is made using an industry-standard Packard/Delphi: Metri-pack 150 connector. (摘自 MINCO 公司網頁)

以及(4) 溫度IC(Temperature sensor ICs, or Silicon based temperature sensor)：近代也有許多積體電路IC就具有溫度量測功能，以下就舉德州儀器公司(Texas Instruments)所生產之LM35為例說明(如下圖，摘自Texas Instruments)：

   

上圖為National Semiconductor公司所出版LM-35 Datasheet的一頁(摘自http://www.jameco.com/Jameco/Products/ProdDS/1276463.pdf，2011年4月4日，德州儀器宣布以65億美元收購National Semiconductor，9月23日兩家公司正式合併 )，下圖則為LM-35使用電路範例。

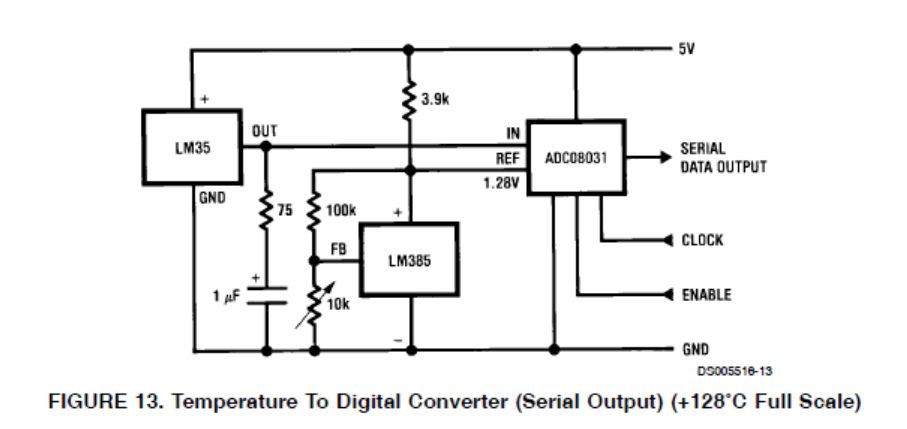
LM-35電路範例(摘自http://www.ti.com/lit/ds/symlink/lm35.pdf )。

上圖中LM35即是輸出為攝氏度的溫度IC，而LM385為可調式微功率參考電壓產生器(Adjustable Micropower Voltage References)，ADC08031則為高速序列輸出之8 bit 類比/數位轉換器(8-Bit High-Speed Serial I/O A/D Converters with Multiplexer Options, Voltage Reference, and Track/Hold Function)。

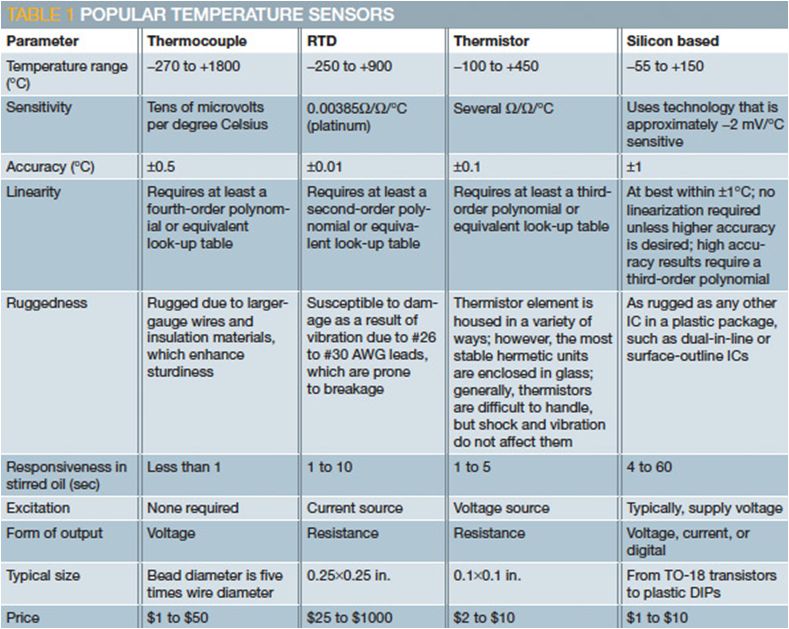
以下為上述四種溫度傳感器之工作範圍、靈敏度、精確度、線性度、堅固度等等性能以及價位之相對評比(摘自Bonnie Baker 2011, Designing with temperature sensors, part one: sensor types)。海洋儀器多使用白金RTD量測溫度，也有一些自動觀測儀器採用溫度IC。 

(三)鹽度量測(電子學方法)

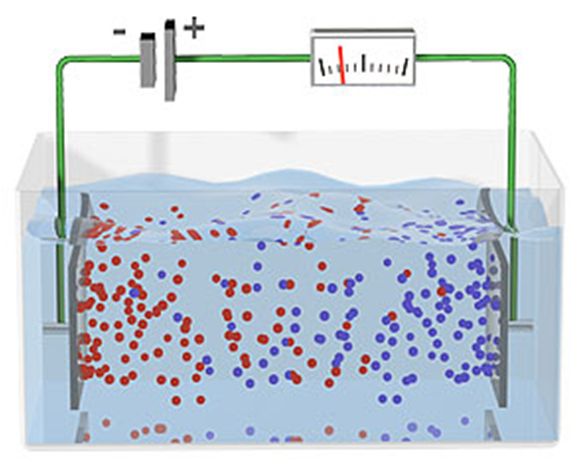
海水鹽度與海水中離子濃度成正比，而海水電阻大小則與海水中離子濃度成反比(導電度conductivity，又或稱電導，為電阻之倒數)，因此海水電導與海水鹽度成正比。電子學裡有一個Pouillet定律(Pouillet's law)，說的是一物體之總電阻R與其截面積A成反比，但與其長度l則成正比，以公式表示便是R = ρ(l/A)，式中之比例係數ρ稱為電阻率 (resistivity)，ρ 之單位為(Ωm) (Ω為歐姆，ohm；電導為電阻之倒數，其單位過去稱為姆歐，mho，但SI units新的名稱係以Siemens 西門子取代姆歐，即 1 Ω^-1 = 1 Siemens)；電阻率之倒數就稱為導電率(conductivity) σ = 1/ρ，故導電率單位為(Ωm)^-1，也就是Siemens per meter (S/m)。

量測海水電導常用的方法不外兩種 ：(1)傳導法(Conductive conductivity measurement)，與(2)電感法(Inductive conductivity measurement)。

(1)傳導法(Conductive conductivity measurement)：將正負電極均置入水中，以電錶直接通電量測水體之電阻再換算成電導(本圖原摘自Endress+Hauser AG 公司網頁，但目前此圖似已下架)。

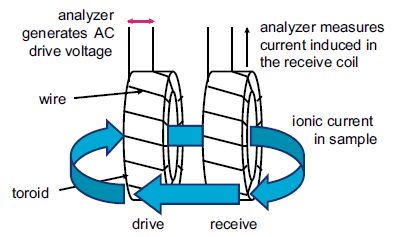
(2)電感法(Inductive conductivity measurement)(本圖原摘自Endress+Hauser AG 公司網頁，但目前此圖似已下架)。 電感法量測導電度之原理類同變壓器(如下圖以及左下圖所示)，係使用兩組平行配置的獨立線圈，二者均需完全浸入待測的海水中，然後以交流訊號驅動其中一組線圈(如下圖左方者，稱為主動線圈)，此時海水樣本(相當於變壓器之鐵心)會產生通過線圈之離子電流，而同時右方線圈(接收線圈)則會生出感應電流，接收線圈感應電流之大小與水體中離子濃度成正比，是以藉此便可以測出水體之電導。 本圖摘自Theory and Application of Conductivity, Application Data Sheet ADS 43-018/rev.D, January 2010.

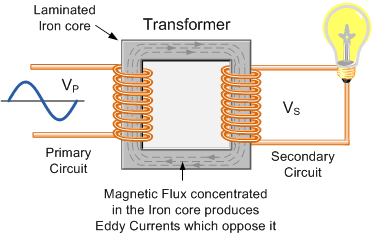變壓器示意圖(摘自ElectronicsTutorials)

1931年法拉第將鐵環兩邊分別用電線纏繞，一端通電之瞬間另端線路也產生電流，他以此實驗証明電磁感應現象(上圖，摘自Wikipedia Faraday's law of induction)，變壓器(左圖)工作原理即是根據法拉第電磁感應定律。純水具有抗磁性，但海水則不然，因此海水可以像變壓器鐵心一樣導磁，然而離子濃度不同會使導磁效率不同，是以經由次級線圈(即前述電感法導電度計之接收線圈)可以感測離子濃度變化。

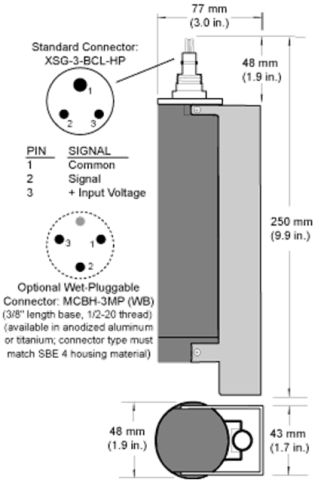
這兩種量測法均各有優缺點，傳導法的優點是感應器可以做得很小，反應快，靈敏度、準確度以及精確度均高，但缺點則是感應器比較脆弱容易受損(例如Neil-Brown CTD的導電度感應器不小心碰到便有可能斷裂)，且感應器電極片必需保持非常潔淨，否則會嚴重影響準確度；由於傳導法感應器電極是直接與海水接觸，很容易受到污染(例如沾上油污，或受生物附著影響)，因此不適宜長期放置海上現場使用，多使用在短期量測裝備(例如CTD，每次下放回收作業最多數小時，如不幸受污回收後可立即檢查清洗)。至於電感法的優缺點則正好與傳導法相反，由於感應器線圈是封裝在保護殼內，比較堅固耐碰撞且並不與外界海水直接接觸，縱使沾上油污或有生物附著均影響甚微，故可安裝在自記儀器(如自記式海流儀、海上浮標等)上放置海中現場長期使用， 但其缺點則在於體積較大、靈敏度與精確度較差，在感應器線圈四周至少3英吋範圍內要避開金屬物(避免電磁感應作用產生渦電流而干擾到接收線圈靈敏度)，同時無法在導電度低(<100 µS/cm，引自 https://www.ibt.kit.edu/english/1210.php)的水體中使用。以下為兩種感應器之實物舉例照片。

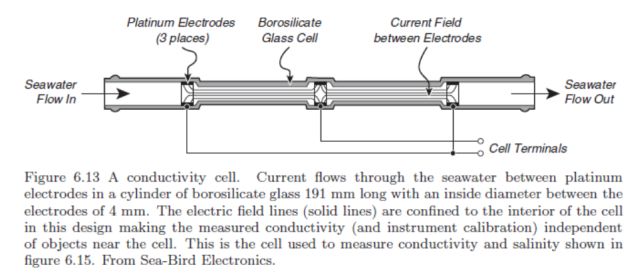美國Sea-Bird公司所製造之傳導式導電度感應器內部架構(摘自Sea-Bird CTD Manual)。 使用傳導法以直流電方式量測海水導電度時，有可能會因電化學作用在電極產生氣泡而造成干擾，為了避免此點，海洋儀器在設計時即多改為使用高頻交流電訊號方式來量測。

Sea-Bird公司SBE 11plus CTD 所用之傳導式導電度感應器，引自 Sea-Bird Data Sheet)

挪威Aanderaa公司RCM流速儀及其它儀器所用之電感式導電度感應器(摘自Aanderaa Conductivity sensor)

(四)運動感應器(Motion sensor, or Motion detector)

俗話說「海上無風三尺浪」，海面上波浪幾乎無時不在，因此不論作業船隻或是觀測儀器(不論船載、錨碇、漂浮或是自行)多半都經常處於搖晃的環境中。有時為了得到更精準的量測值(例如多音束水深測量)需要修正載台搖晃對測量的影響，另外也有些情況，例如使用海面浮體來觀測波浪，就是利用載台的運動情形來反推波浪狀況，因此載台本身的運動姿態(包括方位、前後與左右傾斜、以及垂直方向運動等)便也是一些重要的海洋觀測項目。傳統上是使用羅盤(compass)、加速度計(accelerometer)以及傾斜儀(tilting sensor)等來量測載台或儀器的運動，時至今日這些感應器早已數位化或IC化了，而隨著智慧型手機加入運動感應的功能後，各種輕薄短小的微感應器更是越做越小，響應速度與效能則是越來越快、越來越強，而過去只有單軸的加速度計(例如卅年前的浮球式波浪儀內部即安裝了一個單擺式加速度計)如今IC化的三軸加速度計都早已問世許久(在浮體重心附近安裝三軸加速度計、數位羅盤以及水平雙軸傾斜儀便可以充份掌控到浮體運動的完整訊息)，以下為加速度計的一些簡要說明。

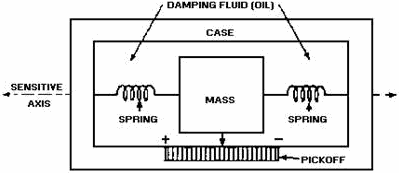	一個最簡單的加速度計示意圖，摘自 Navy Electricity and Electronics Training Series (NEETS) Module 15—Principles of Synchros, Servos, and Gyros
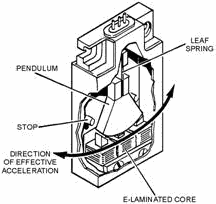	E-transformer加速度計，以E型變壓器的鐵心作為懸在單擺下之擺錘質量，整體密封浸在油中以避免單擺振動，摘自 Navy Electricity and Electronics Training Series (NEETS) Module 15—Principles of Synchros, Servos, and Gyros 。早期浮球式波浪儀所用之加速度計應與此類似。

以ANALOG DEVICES公司製造之ADXL354/ADXL355三軸加速度計IC為例，其主要特性有： Hermetic package offers excellent long-term stability, 0 g offset vs. temperature (all axes): 0.15 mg/°C maximum, Ultra-low noise density (all axes): 20 µg/√Hz, Low power, VSUPPLY (LDO enabled), 150 µA in measurement mode (digital), 21 µA in standby mode, ,Digital serial peripheral interface (SPI)/I2C interfaces,  20-bit analog-to-digital converter (ADC), Operating temperature range: -40°C to 125°C, 14-terminal, 6 mm x 6 mm x 2.1 mm LCC package, weighing 0.26 g. 摘自 ADXL354/ADXL355 3-Axis Mems Accelerometers。

將垂直加速度對時間積分後便是垂直速度，將垂直速度再對時間積分則是垂直位移。如果浮體能保持在海面上且浮體中心的垂直軸能夠維持與波平面垂直，那麼經由三軸加速度以及數位羅盤給出之方位等資料便可反算出波面之垂直位移以夃波面之傾角與波面法線方向，如此即可得出波高與波向。近代許多海上觀測浮台(例如中央氣象局的海象觀測浮標)都是使用這種方式量測海洋波浪。

物理海洋學現場觀測參數項目當然遠遠不止這些，在隨後各節我們還將隨時再行補充相關材料，不過在結束本節前，由於和海流一些觀測方法原理有關，所以我們有必要在此複習一下都卜勒效應，以及「法拉第電磁感應定律」，這些在隨後第三、四節會再用到。

(五)都卜勒效應(Doppler effect)

高中物理上冊提到「當觀察者與波源兩者在其連線上有相對運動時，觀察者所測得的頻率(視頻率 n )與波源實際上所發出之頻率(f)不同，這種現象稱為都卜勒效應」，例如「當救護車接近觀察者時，頻率較原來者高」，而「當救護車遠離觀察者時，頻率較原來者低」；以及「當火車減速進站時，音調將由高逐漸變低」等等；「如波速為V，而沿觀察者與波源之連線上，波源的速度為Vs，觀察者的速度為Vo。則視頻率 n = f (V ± Vo)/(V± Vs) (波源與觀察者二者速度如與波速同向取負，反之則取正)」。聲學方法在各種海洋探測裝置中常扮演重要的角色，以下就以聲波為例來說明。

左圖(摘自The Doppler Effect and Sonic Booms, Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University)顯示一個固定不動之聲源所發出聲波之示意圖，聲波為非離散波(non-dispersive waves，參見第七章)，其波速V為介質特性(例如溫度)的函數，不因波長或頻率不同而改變。令波速為V，波長為L，波週期為T (頻率 f = 1/T)，V=L/T；假設在時間t = 0時正好有一波峰通過觀測者，此時下一個波峰與觀測者之距離則為L，假若觀察者是以Vo的速度向著聲源前進，那麼在 t = L/(V+Vo)時，此觀察者將遇到下一個波峰，這個時間間隔便是觀察者所「看到」波的視週期P(其倒數即為視頻率n，n=1/P)，故 P = L/(V+Vo) = (V/f)/(V+Vo)，或 n = f (V+Vo)/V，因此知視頻率n會較聲源所發出之頻率高。同理，如觀察者為向著離開波源的方向行進，則n = f (V-Vo)/V，視頻率n會較聲源所發出之頻率低。在此例中聲波波長L係保持固定不變。

如果觀察者在空間中保持固定不動，換由聲源以Vs的速度向著觀察者前進，聲源仍然以週期T的間隔產生聲波，聲波的波速為V。假設在t = 0時正好有一個波峰離開聲源，而到 t = T時又會再生出下一個波峰離開；由於聲波離開聲源後是以V的速度行進，而聲源則以Vs的速度同向跟進(假設Vs < V)，因此間隔T時間後兩個波峰之間的距離(就是外觀波長Lo)為：Lo=(V-Vs)T，是以外觀波長Lo會因波源在運動而改變，但聲速V需為定值，因此波長為Lo之聲波所對應之頻率為n(對應關係為n = V/Lo，此式就是由波速關係式而來的；令To=1/n，則V = Lo/To)，便可得出 Lo = V/n = (V-Vs)T= (V-Vs)/f，也就是n = fV/(V-Vs)，視頻率n亦為較聲源所發出之頻率高。反之如聲源離觀察者而去，則為n = fV/(V+Vs)，視頻率n為較聲源所發出之頻率低。在此例中聲波波長會發生改變。左圖即為聲源以0.7倍音速向右移動情況之示意圖(摘自The Doppler Effect and Sonic Booms, Daniel A. Russell, Graduate Program in Acoustics, The Pennsylvania State University)

將上面兩個例子結合後便可得出前述「視頻率 n = f (V ± Vo)/(V± Vs)」之關係式，雖然在定性上，不論觀察者動或是波源動，只要二者在其連線間有相對運動都會產生都卜勒效應；但是就波長而言，觀察者動或是波源動還是有著本質上的差異。如波源不動，由波源輻射出去的波其波長與頻率均穩定不變，此時因觀察者移近、移遠所產生的效應僅是觀察者自身在單位時間內所接收到波的數目(外觀頻率)之改變，但波長仍是原波長；可是如果波源本身也向著波傳方向移動，此時由波源向四周輻射的波本身(波長與頻率)就會發生改變，這就是最重要的差異。

當代海洋研究船上都裝有一項稱為「聲學式都卜勒海流剖面觀測儀 (Acoustic Doppler Current Profiler)」的重要海流觀測裝備，便是利用聲波的都卜勒效應來量測海流剖面；另外岸基高頻雷達(Land-based High-Frequency Radar)也是利用雷達波去測量海面波浪頻率受海流影響所發生的都卜勒效應而得出海面海流分佈；又如飛機或人造衛星上裝載之合成孔徑雷達(Synthetic Aperture Radar, SAR)可以得到解析度非常高的地表或海表圖像，SAR的成像原理也要用到都卜勒效應。這些我們會在第四節再予介紹。

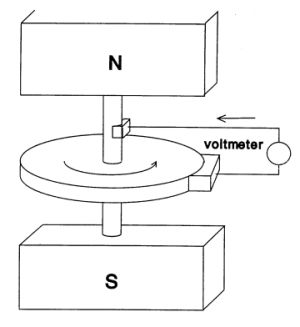
(六)法拉第電磁感應定律(Faraday's Law of Induction)

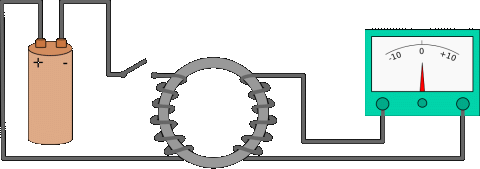
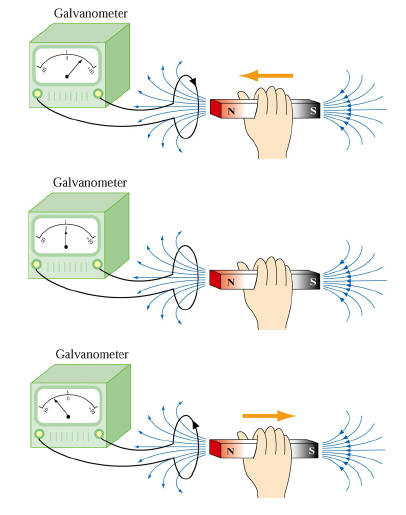
「法拉第電磁感應定律」指的是：「任何封閉電路中感應電動勢的大小，等於穿過這一電路磁通量的變化率」。1831年法拉第發現如果讓磁場隨時間變動，那麼就可以產生電場，這種現象稱作「電磁感應 (Electromagnetic induction)」。

麥可·法拉第 (Michael Faraday FRS，1791 9/22 - 1867 8/25)，出身寒微沒受過什麼正式教育，卻成為偉大的實驗物理科學家，在電磁學及電化學等領域(主要在電磁感應、電解作用、抗磁性等方面)都有很多重要貢獻，是人類科學史上最具有影響力的科學家之一 。(引自Wikipedia Michael Faraday) 法拉第電磁感應實驗示意圖(摘自Faraday's Law of Induction, the course notes of Physics 8.02 Electricity and Magnetism at MIT )。1831年法拉第用這樣的實驗解說電磁感應現象：(上)將長條磁鐵向封閉線圈電路中央移進，電流計顯示電路中出現電流；而磁鐵停止不動電流亦停止(中)；若磁鐵向遠離線圈方向移動時則電路中出現反向電流(下)。這個實驗証明若磁場隨時間改變可以在封閉迴路的導體內產生電流(反之若磁場不變，移動導體也會產生同樣的效應)，這就是電磁感應。因此如果磁鐵與導體二者能一直維持著相對運動且導體可以不斷切割磁力線，那麼在垂直於磁力以及導體相對運動方向的兩端就會有電位差，如果將兩端以導線相連，導線內便會有電流。法拉第依此原理設計了一個發電裝置(如下左圖)，後人稱為法拉第輪(Faraday's disk or Faraday's wheel)。

左圖為法拉第輪(摘自Wikipedia Homopolar generator)，是人類歷史上的第一台直流發電機。右圖則為其工作原理之示意圖(摘自The Dynamo Process)；在銅盤上下方分別放置磁鐵的兩極，當銅盤旋轉運動時，因導體正向切割磁鐵兩極間的磁力線，電磁感應作用將使銅盤外側與銅盤轉軸間產生電位差，此時若用導線連接銅盤內、外側就會有電流通過導線。

1817年時的倫敦Waterloo橋(摘自Waterloo Bridge)，1832年法拉第在此橋橋孔兩端量測泰晤士河退潮流因地球磁場感應產生之電位差。

摘自Michael Faraday's Waterloo Bridge Experiment

(摘自The Dynamo Process)

1832年法拉第認知到，帶離子的水(例如海水或倫敦泰晤士河受海潮影響的河水)是導體，因此在地球磁場作用下，這種水的水流也有可能成為流體發電機(fluid dynamos))，因此他在泰晤士河Waterloo橋進行實驗(於橋孔兩端將白金電極放入河水中，然後用導線相連)，藉以量測泰晤士河退潮流受地球磁場感應作用產生之電位差(如左圖)。雖然由於種種原因(電極在水中因電化學反應所造成的電位變化遠大於流體發電機所能產生的電位變化，這種干擾未能避免；另方面也因法拉第時代的電錶量不出這麼些微的電位變化)實驗並不成功，但他的想法確是可行的，現代使用的電磁式海流儀以及工業界仍在廣泛使用的電磁式流量計皆源自於法拉第的原始構想。

流體發電機發電原理示意圖(摘自Magneto hydro dynamic (mhd) power generation)，左圖中橘色平板為感應電極(上板為陰極，下板為陽極)，灰色平板為絕緣板，紅色水平箭頭表示磁力方向，藍色箭頭表示流體流動方向，電路上的紅色箭頭表示電子流方向。當代電磁式海流儀以及電磁式流量計在設計架構上與此圖所示雖有差異，但也是應用同樣的電磁感應原理來測量流速。

本章始建於1998/9/17, revised: 2017/3/21